2026 January 13th. How to use math to fold a pentagon

Deriving the Pentagon Fold Using the Golden Ratio

To fold a regular pentagon from paper, the key quantity is the exact value of
$\cot 72^\circ$cot72∘, which is deeply connected to the golden ratio.

---

Exact Value of $\cot 72^\circ$cot72∘

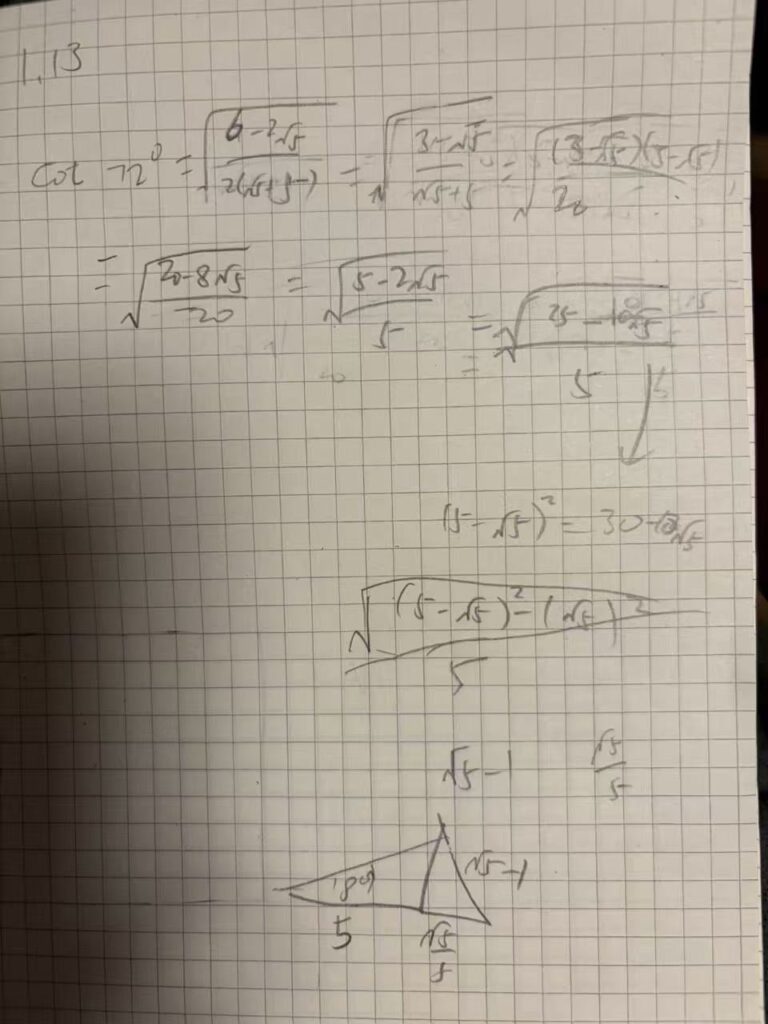
We start with the identity:$$\cot 72^\circ = \sqrt{\frac{5 – 2\sqrt{5}}{5}}$$cot72∘=55−25​​​

Notice that:$$(\sqrt{5} – 1)^2 = 6 – 2\sqrt{5}$$(5​−1)2=6−25​

So the expression simplifies as:$$\cot 72^\circ = \sqrt{\frac{(\sqrt{5} – 1)^2}{5}} = \frac{\sqrt{5} – 1}{\sqrt{5}}$$cot72∘=5(5​−1)2​​=5​5​−1​

---

Connection to the Golden Ratio

The golden ratio is defined as:$$\varphi = \frac{1 + \sqrt{5}}{2}$$φ=21+5​​

Its reciprocal is:$$\frac{1}{\varphi} = \frac{\sqrt{5} – 1}{2}$$φ1​=25​−1​

Therefore:$$\cot 72^\circ = \frac{2}{\sqrt{5}} \cdot \frac{1}{\varphi}$$cot72∘=5​2​⋅φ1​

This shows that the folding ratio is governed by the golden ratio.

---

Geometric Interpretation

If a segment of length $1$1 is used as the base, then folding at an angle of
$72^\circ$72∘ with height:$$h = \frac{\sqrt{5} – 1}{\sqrt{5}}$$h=5​5​−1​

produces the exact proportions needed for a regular pentagon.

This explains why pentagon paper-folding constructions naturally involve
$\sqrt{5}$5​ and the golden ratio.

Mathematical Idea (Why This Works)

A regular pentagon has interior angles of $108^\circ$108∘, so the exterior angle is:$$180^\circ – 108^\circ = 72^\circ$$180∘−108∘=72∘

The crucial ratio used in the fold is:$$\cot 72^\circ = \frac{\sqrt{5} – 1}{\sqrt{5}}$$cot72∘=5​5​−1​

This ratio is directly related to the golden ratio:$$\varphi = \frac{1+\sqrt{5}}{2}$$φ=21+5​​

This is why pentagon folding always involves $\sqrt{5}$5​.

---

Step-by-Step Folding Instructions

---

Step 1: Start with a Square

Begin with a square sheet of paper.

If your paper is rectangular:

• Fold one corner diagonally
• Trim or fold away the excess to make a square

---

Step 2: Fold the Square in Half Horizontally

• Fold the square in half left-to-right
• Crease well
• Open the paper

This center line will be your reference axis.

---

Step 3: Create the Golden Ratio Point

1. Fold the bottom left corner to the midpoint of the right edge
2. Crease firmly
3. Open the paper

This fold creates a point that divides the base in the golden ratio.

This is the geometric origin of:$$\frac{\sqrt{5}-1}{\sqrt{5}}$$5​5​−1​

---

Step 4: Form the 72° Folding Line

• From the golden-ratio point, fold a line upward to meet the top edge
• Adjust until the fold aligns naturally
• Crease firmly

This fold is exactly at 72∘72^\circ72∘ relative to the base.

You are now physically constructing$$\cot 72^\circ = \frac{\sqrt{5}-1}{\sqrt{5}}$$cot72∘=5​5​−1​

---

Step 5: Lock the Pentagon Shape

• Fold the paper along this $72^\circ$72∘ line
• Then repeat the fold symmetrically on the opposite side
• The edges will begin forming a five-sided symmetry

---

Step 6: Final Collapse

• Carefully fold the remaining flaps inward
• Align all edges
• Press flat

When unfolded or trimmed, the shape formed is a regular pentagon.

---

Why the Pentagon Appears Automatically

The folds enforce:

• Equal edge lengths
• Exact $72^\circ$72∘ angles
• Golden-ratio proportions

This happens without measuring, because the paper geometry encodes:$$(\sqrt{5}-1)^2 = 6 – 2\sqrt{5}$$(5​−1)2=6−25​

which controls pentagonal symmetry.

---

Summary

• Pentagon folding is governed by $\sqrt{5}$5​
• The golden ratio appears naturally
• The key angle is $72^\circ$72∘
• Paper folding performs exact irrational geometry