Steven’s notebook from 2026 January 12th.
He decided to use a new notation to express the sumation of terms. Below includes the extracted info and the original hand writen notes
Basic Sums of Powers
Definition
We define a summation operator for a function f(x):S(f)=x=1∑nf(x)
Our goal is to compute sums of the form:x=1∑nxk
1. Constant Function
S0=x=1∑n1=n
2. Linear Function
S1=x=1∑nx
The pairing trick
x=1∑nx=21x=1∑n(x+(n+1−x))
Since each pair sums to n+1, we obtain:S1=2n(n+1)
3. A Key Telescoping Identity
Consider the difference:xk−(x−1)k
Summing from x=1 to n:x=1∑n(xk−(x−1)k)=nk
This identity is the foundation of the method.
4. Binomial Expansion
Using the binomial theorem:(x−1)k=i=0∑k(ik)xi(−1)k−i
Therefore,xk−(x−1)k=−i=0∑k−1(ik)(−1)k−ixi
5. Recurrence Formula for Power Sums
Summing both sides and rearranging gives:x=1∑nxk=k+11nk+1−i=0∑k−1k+11(ik+1)x=1∑nxi
This expresses a power sum in terms of lower-degree sums.
6. Example: Sum of Squares
Let k=2.x=1∑nx2=31n3−31((03)∑1+(13)∑x)
Substituting known sums:=31n3−31(n+3⋅2n(n+1))
Simplifying:x=1∑nx2=31n3+21n2+61n
Which factors as:x=1∑nx2=6n(n+1)(2n+1)
7. Summary
- Constant sums are linear in n
- Linear sums are quadratic in n
- Power sums satisfy a recursive formula
- All polynomial sums can be derived using telescoping + binomial expansion

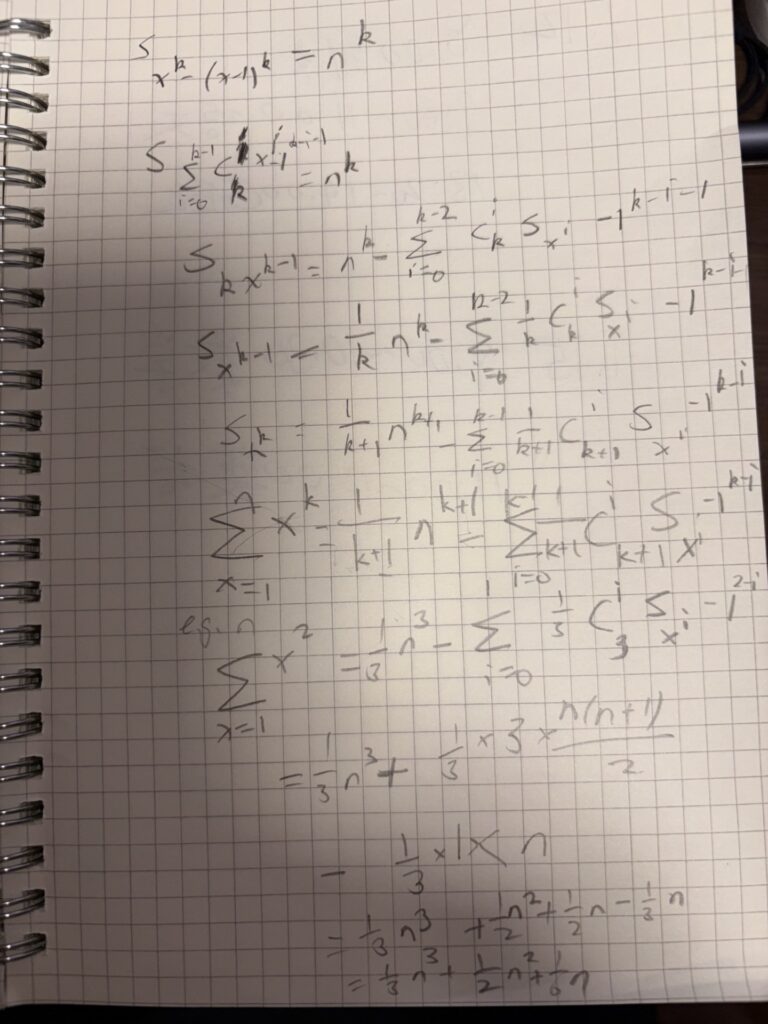
Amazing!!